5017: Jeffery_Li的特殊排序

题目描述

$Jeffery\_Li$有$T$个数组，他要分别对这些数组进行排序。
其中第$i$个数组中有$n_i$个数。
$Jeffery\_Li$需要通过交换数字来使得数组变得有序，但是交换数字是有限制的：
如果要交换两个数字，$Jeffery\_Li$需要找到第三个数，使得它在数组里的位置到需要交换的两个数距离相同（详细见样例解释）。
$Jeffery\_Li$如果能将这组数从小到大排序完毕，输出YES，否则输出NO。

输入格式

第一行一个整数$T$。
接下来$T$组输入，每组第一行一个整数$n_i$，表示这个数组的大小。
接下来一行$n_i$个整数，表示这个数组的每个元素。

输出格式

每组数据输出一行一个字符串，如果能将数组从小到大排序完毕，则输出"YES"，否则输出"NO"。

样例 #1

样例输入 #1 复制

6
2
16 29
3
1 16 29
5
1 30 35 4 4
6
28 30 16 1 15 2
9
999 20 2024 1314 15 520 666 888 38
11
2024 10 1 5 1 2 10 5 18 1000000007 10000000095

样例输出 #1 复制

YES
YES
YES
NO
YES
NO

提示

【样例解释】

对于样例中的第三组数字，$Jeffery\_Li$可以先交换$30$和$4$，它们的下标分别位$2$和$4$，其中$35$到它们的距离相同，都为$1$，所以$Jeffery\_Li$可以交换这两个数字。
数组变为：$1 \space 4 \space  35 \space  30 \space 4$
之后$Jeffery\_Li$可以交换$35$和$4$，使得数组变为：$1 \space 4 \space  4 \space  30 \space 35$。(如下图)

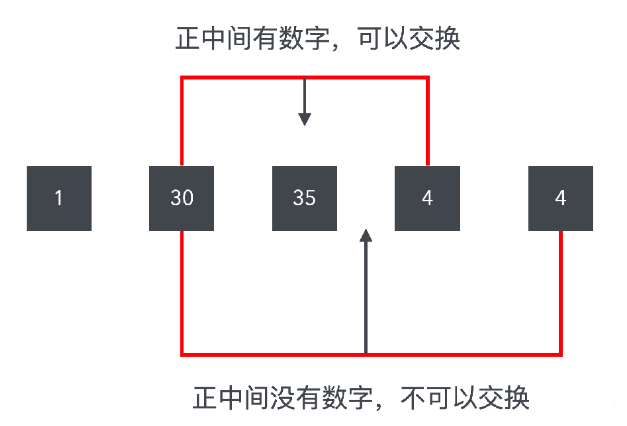
【数据范围】

对于所有数据：$1 \leq T \leq 20,1 \leq a_i \leq 10^{18}$，保证所有数组大小的和$\sum n_i$不超过$3 * 10^5$。
|测试点编号|特殊限制|
|$1 \sim 3$|$1 \leq n_i \leq 3$|
|$4 \sim 6$|$1 \leq n_i \leq 7$|
|$7 \sim 20$|$1 \leq n_i \leq 10^5$|