4048: 「AHOI / HNOI2017」单旋

H 国是一个热爱写代码的国家，那里的人们很小去学校学习写各种各样的数据结构。伸展树（splay）是一种数据结构，因为代码好写，功能多，效率高，掌握这种数据结构成为了 H 国的必修技能。有一天，邪恶的「卡」带着他的邪恶的「常数」来企图毁灭 H 国。「卡」给 H 国的人洗脑说，splay 如果写成单旋的，将会更快。「卡」称「单旋 splay」为「spaly」。虽说他说的很没道理，但还是有 H 国的人相信了，小 H 就是其中之一，spaly 马上成为他的信仰。 而 H 国的国王，自然不允许这样的风气蔓延，国王构造了一组数据，数据由 $m$ 个操作构成，他知道这样的数据肯定打垮 spaly，但是国王还有很多很多其他的事情要做，所以统计每个操作所需要的实际代价的任务就交给你啦。 数据中的操作分为五种： 1. 插入操作：向当前非空 spaly 中插入一个关键码为 $\mathrm{key}$ 的新孤立节点。插入方法为，先让 $\mathrm{key}$ 和根比较，如果 $\mathrm{key}$ 比根小，则往左子树走，否则往右子树走，如此反复，直到某个时刻，$\mathrm{key}$ 比当前子树根 $x$ 小，而 $x$ 的左子树为空，那就让 $\mathrm{key}$ 成为 $x$ 的左孩子； 或者 $\mathrm{key}$ 比当前子树根 $x$ 大，而 $x$ 的右子树为空，那就让 $\mathrm{key}$ 成为 $x$ 的右孩子。该操作的代价为：插入后，$\mathrm{key}$ 的深度。特别地，若树为空，则直接让新节点成为一个单个节点的树。（各节点关键码互不相等。对于「深度」的解释见末尾对 spaly 的描述）。 2. 单旋最小值：将 spaly 中关键码最小的元素 $\mathrm{xmin}$ 单旋到根。操作代价为：单旋前 $\mathrm{xmin}$ 的深度。（对于单旋操作的解释见末尾对 spaly 的描述）。 3. 单旋最大值：将 spaly 中关键码最大的元素 $\mathrm{xmax}$ 单旋到根。操作代价为：单旋前 $\mathrm{xmax}$ 的深度。 4. 单旋删除最小值：先执行 2 号操作,然后把根删除。由于 2 号操作之后,根没有左子树,所以直接切断根和右子树的联系即可（具体见样例解释）。 操作代价同 2 号操作。 5. 单旋删除最大值：先执行 3 号操作,然后把根删除。 操作代价同 3 号操作。  对于不是 H 国的人，你可能需要了解一些 spaly 的知识，才能完成国王的任务： - spaly 是一棵二叉树，满足对于任意一个节点 $x$，它如果有左孩子 $\mathrm{lx}$，那么 $\mathrm{lx}$ 的关键码小于 $x$ 的关键码。如果有右孩子 $\mathrm{rx}$，那么 $\mathrm{rx}$ 的关键码大于 $x$ 的关键码。 - 一个节点在 spaly 的深度定义为：从根节点到该节点的路径上一共有多少个节点（包括自己）。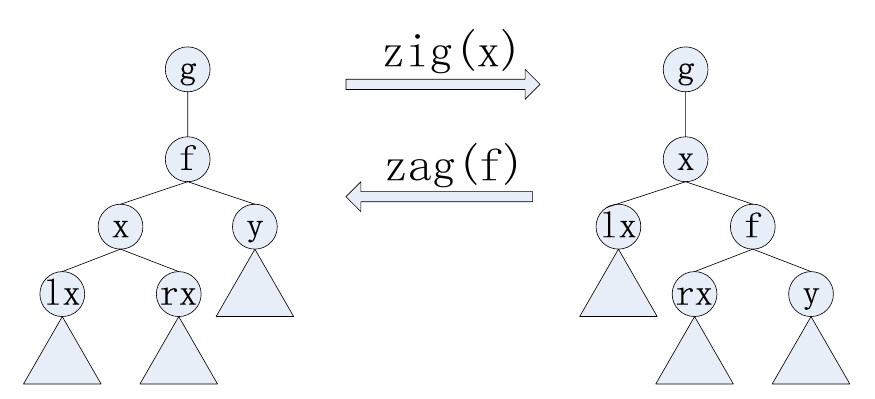 - 单旋操作是对于一棵树上的节点 $x$ 来说的。一开始,设 $f$ 为 $x$ 在树上的父亲。如果 $x$ 为 $f$ 的左孩子，那么执行 $\mathrm{zig}(x)$ 操作（如上图中，左边的树经过 $\mathrm{zig}(x)$ 变为了右边的树），否则执行 $\mathrm{zag}(x)$ 操作（在上图中，将右边的树经过 $\mathrm{zag}(f)$ 就变成了左边的树）。每当执 行一次 $\mathrm{zig}(x)$ 或者 $\mathrm{zag}(x)$，$x$ 的深度减小 $1$，如此反复，直到 $x$ 为根。总之，单旋 $x$ 就是通过反复执行 $\mathrm{zig}$ 和 $\mathrm{zag}$ 将 $x$ 变为根。

第一行单独一个正整数 $m$。 接下来 $m$ 行，每行描述一个操作：首先是一个操作编号 $c\in [1, 5]$，即问题描述中给出的五种操作中的编号，若 $c = 1$，则再输入一个非负整数 $\mathrm{key}$，表示新插入节点的关键码。

输出共 $m$ 行，每行一个整数，第 $i$ 行对应第 $i$ 个输入的操作的代价。

5
1 2
1 1
1 3
4
5

1
2
2
2
2