3985: 「LibreOJ Round #6」花煎

> 「Mix it well!」 > > 对于 Alice 来说，与 Shinobu 的初识，以及一同制作的曲奇饼，都将是她永远珍藏的回忆。 > > 而 Shinobu 对于外国文化的强烈憧憬总能使她与 Alice 找到更多新奇的活动 —— 这次，是来自邻居国度的「花煎游戏」。 > > 「花煎」来自于朝鲜半岛传统，以米饼上放置可食用的时花制成，而「花煎游戏」是指郊游踏青时采花制作花煎的活动，后来渐渐与源自中国的「重阳」习俗结合。 > > 两人很快便兴致勃勃地开始了制作，不过 Alice 似乎很想在 Shinobu 面前展示自己最好的一面…… > > Alice 希望将自己制作的所有花煎摆成一个圆环形，并且使它们的色彩尽可能地丰富。由于 Alice 还要忙着制作，所以她把问题进行了一些抽象，希望擅长程序设计的你可以为她解决。 一个环由 $n$ 个元素组成，顺时针标号为 $1$ 至 $n$，其中 $n$ 为**不小于 $\mathbf{4}$ 的偶数**。每个元素都有一个颜色，且第 $i$ 个元素的颜色居下列二者之一： 1. 除元素 $i$ 外的其他元素均与 $i$ 不同色，Alice 称元素 $i$ 为「独立」的； 2. 除元素 $i$ 外有且仅有元素 $i + \frac n 2$ 或 $i - \frac n 2$（其中恰有一个在编号范围内）与 $i$ 同色，Alice 称元素 $i$ 为「对立」的。 定义一个环的**色彩值**为**所有被「对立」元素分开的子段的长度乘积**。换言之，将所有的「对立」元素移除，色彩值等于剩余的环上连续子段（包括长度为 $0$ 的子段 —— 出现在两个「对立」元素相邻的情况下）的长度乘积。特别地，如果环上没有「对立」元素，那么其色彩值为 $0$。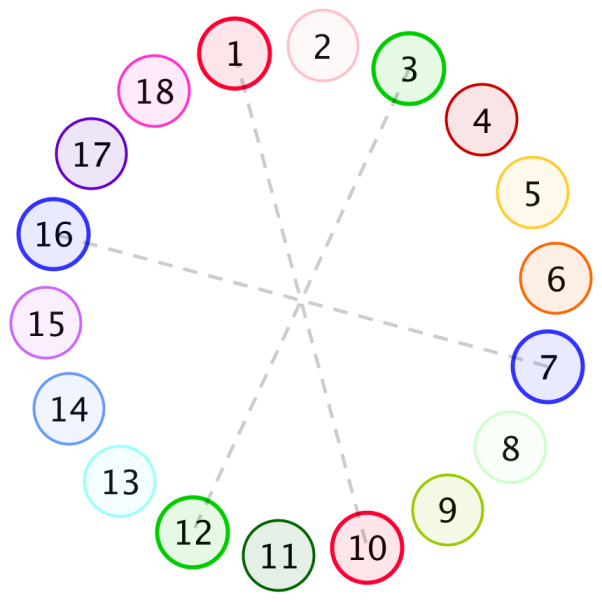
现在 Alice 想获得一个色彩值**不小于** $m$ 的环。Alice 想请你帮忙计算这样一个环的最小大小 —— Alice 仍旧犹豫不定，因此你需要对于 $T$ 个这样的 $m$ 分别进行计算。

输入的第一行包含一个正整数 $T$ —— 需要计算的 $m$ 的个数。 接下来 $T$ 行，每行包含一个正整数 $k$ —— 由于 $m$ 可能很大，输入的值表示它的**正平方根**，即 $m = k^2$。

输出 $T$ 行 —— 对于每个输入的 $k$ 输出一行，包含一个整数，表示色彩值不小于 $k^2$ 的环最少包含的元素个数。当然啦，一定是个偶数。

4
5
10
221
1317

12
18
40
54