5570: Adjacent Squares相邻方格(ABC250A)
内存限制:1024 MB
时间限制:2.000 S
评测方式:文本比较
命题人:
提交:0
解决:0
题目描述
Problem Statement:
There is a grid with $H$ horizontal rows and $W$ vertical columns. Let $(i,j)$ denote the square at the $i$-th row from the top and the $j$-th column from the left.
Find the number of squares that share a side with Square $(R, C)$.
Here, two squares $(a,b)$ and $(c,d)$ are said to share a side if and only if $|a-c|+|b-d|=1$ (where $|x|$ denotes the absolute value of $x$).
There is a grid with $H$ horizontal rows and $W$ vertical columns. Let $(i,j)$ denote the square at the $i$-th row from the top and the $j$-th column from the left.
Find the number of squares that share a side with Square $(R, C)$.
Here, two squares $(a,b)$ and $(c,d)$ are said to share a side if and only if $|a-c|+|b-d|=1$ (where $|x|$ denotes the absolute value of $x$).
有一个网格,包含$H$行和$W$列。让$(i,j)$表示从上往下数第$i$行、从左往右数第$j$列的方格。
找出与方格$(R,C)$共享一条边的方格数量。
这里,两个方格$(a,b)$和$(c,d)$被认为共享一条边当且仅当$|a-c|+|b-d|=1$(其中z表示的绝对值)。
输入
Input is given from Standard Input in the following format:
```
$H$ $W$
$R$ $C$
```
输出
Print the answer as an integer.
样例输入 复制
3 4
2 2样例输出 复制
4提示
Constraints:
- All values in input are integers.
- $1 \le R \le H \le 10$
- $1 \le C \le W \le 10$
Sample Input 2
```
3 4
3 4
```
Sample Output 2
```
2
```
When $H=3$ and $W=4$, the grid looks as follows.
- For Sample Input $1$, there are $4$ squares adjacent to Square $(2,2)$.
- For Sample Input $2$, there are $3$ squares adjacent to Square $(1,3)$.
- For Sample Input $3$, there are $2$ squares adjacent to Square $(3,4)$.
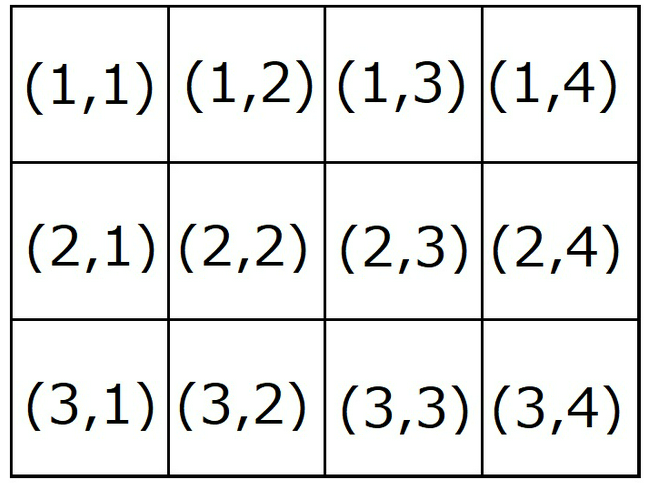
【样例1、2、3说明】
当H=3且W=4时,网格如下所示。
-
对于样例输入1,有4个方格与方格(2,2)相邻。
-
对于样例输入2,有3个方格与方格(1,3)相邻。
-
对于样例输入3,有2个方格与方格(3,4)相邻。